Neuroscience Notes - Neuronal excitability

September 22, 2020 9 分钟读完

Notes taken form Neuroscience course, Part 2: Neuronal excitability.

Last update: Oct. 21, 2020

Translation of Terms

Eng	Chs	Comment
dendrite	树突
axon	轴突
synapse	突触
myelin sheath	髓鞘
vagus nerve	迷走神经
ionotropic
exocytosis	胞外分泌
vesicle	泡，囊
ionotropic	离子移变的
acetylcholine	乙酰胆碱	ACh
hippocampus	海马体	info -> mem
spinal cord	脊髓

Potentials

Membrane Potential

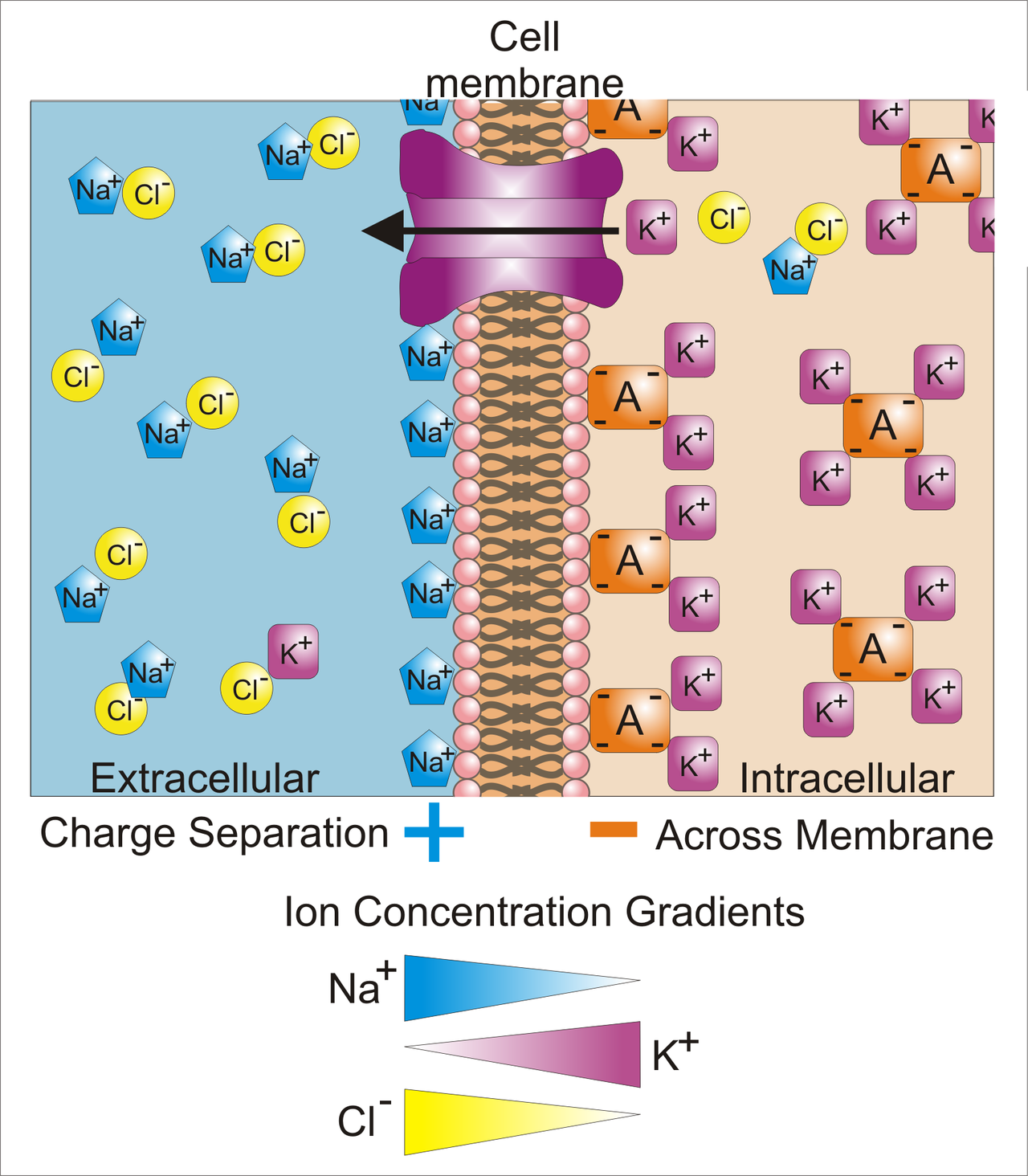
ion pump: brings $K^+$ in and pushes ${Na}^+$ out.

Two forces on ions:

Diffusion high -> low concentration $E_d = RTln([K^+]_o/[K^+]_i)$
Coulomb: opposites attract; like charges repel $E_c = V_zF$
For $K^+$, At equilibrium: $E_c = E_d$

But different ion channels cause different permeabilities for each ion. Therefore we need to times the permeability as weight to each ion when calculating the membrane potential.

Depolarization: a change within a cell, during which the cell undergoes a shift in electric charge distribution, resulting in less negative charge inside the cell.
Hyperpolarization: a change in a cell’s membrane potential that makes it more negative.

i-on channel

${Na}^+$ channel: voltage gated (neg potential -> closed gate)
Depolarization: positive feedback of ${Na}^+$ channel

Membrane depolarization
increase in $g_{Na^+}$
more ${Na}^+$ rushes into cell
lead to 1 => positive feedback

However, $K^+$ behave differently => No feedback

Electrophysiology

Current: $I =\Delta Q/\Delta t$
Ohm’s law
Abstract neuron as circuit: pumps(voltage src) - switch // resistor // capacitor

Hodgkin & Huxley

Energy Barrier Model

Gate: voltage dependence, time dependent
双向流动的模型：$dy/dt = \alpha(1-y)-\beta y$ => $y_{\infty} = \alpha/(\alpha + \beta)$

      	β
open(y) ⇋ closed(1-y) => y∞ (steady state)
        α

Hodgkin and Huxley’s Model

ref: wiki_HHModel

Experiment on squid giant axon with voltage clamp
a brief inward current followed by a longer outward current
TTX blocking $Na^+$ channels and TEA blocking $K^+$ channels => separate the current of each type of channels

Synaptic Transmission

Electrical synapses
Chemical synapses

Otto Loewi’s Experiments

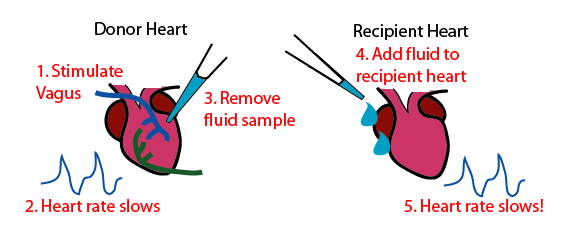
wiki_loewi

Two hearts
stimulate one’s vagus nerve
transfer the solution to heart 2
both of these two heart rates slows

Bernard Katz’s Experiments

mEPP: miniature end plate potential

Action potential needs to reach the threshold (EPP)
mEPPs are spontaneous
EPPs are evoked!
=> quantal hypothesis: probability; quantum; evoked EPP by several quanta

Quantal Analysis

number of packets released $m = V_{EPP}/V_{mEPP}$
release of quanta: follow a Poisson distribution: $P(x) = m^xe^{-m}/x!$
=> counting the times evoked EPPs deliver no transmitter => P(0) => m
=> vesicles were the transmitter quanta

Chemical Synaptic Transmission

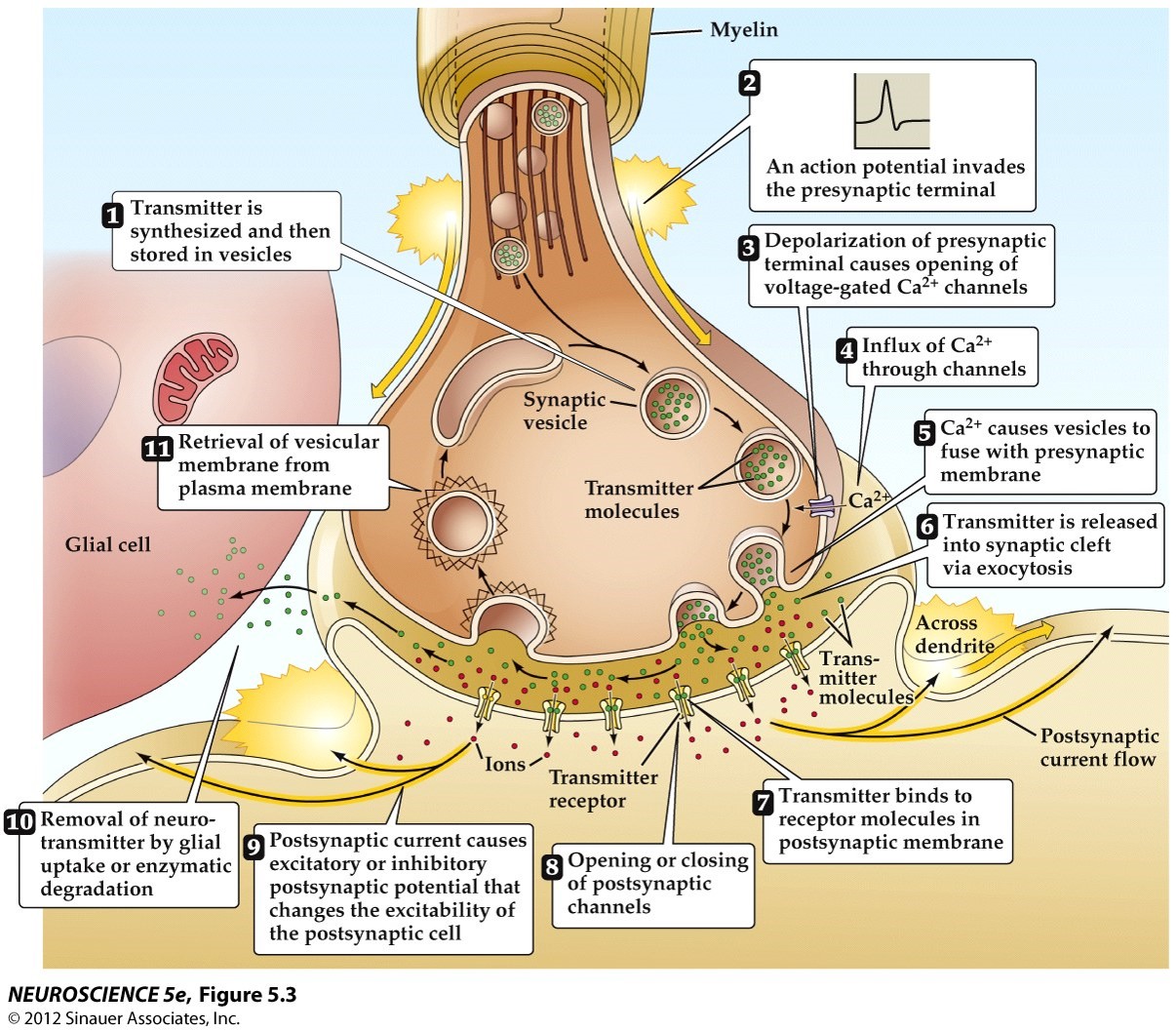
chemTrans

$Na^+$ in, $K^+$ out => Synapse
voltage-gated channels open => $Ca^{++}$ in
vesicles to fuse with membrane => release transmitter that diffuse across the synaptic cleft
transmitter molecules reach receptors (postsynaptic) => open channels and letting in ions
synaptic vesicles in presynaptic terminals can be recycled

Two Categories:

Ionotropic: fast, local channel-mediated changes in membrane potential (EPSPs, IPSPs)
Metabotropic: slow, G-protein- and second-messenger- mediated changes

Benifits of chemical transmission

Graded vs. all-or-none: analog vs. digital
Amplification
Sign inversion
Varied temporal duration
Multiple receptors with distinct properties
Malleability/plasticity

Synaptic Reversal Potentials

EPC: end plate current, the macroscopic current resulting from the summed opening of many ion channels
reversal potential: the membrane potential at which a given neurotransmitter causes no net current flow of ions through that neurotransmitter receptor’s ion channel.
$Ca^{2+}$ entry through the specific voltage-dependent calcium channels in the presynaptic terminals causes transmitter release
a rise in presynaptic Ca2+ concentration triggers transmitter release from presynaptic terminals

Gap Junctions

Electrical Synapse

Synaptic plasticity

plasticity

Short-term

May conduct synaptic computation
May serve as a frequency filter

Facilitation

The 2nd pulse is larger. => the amount = $A2/A1$

Synapse has a low initial probability of transmitting.
Later pulses, letting in more $Ca^{++}$, allow vesicles to move forward => second pulse larger

Depression

just opposite case of facilitation

Model

Amplitude $A = A_0FD$
Facilitation para: $F \rightarrow F+f$
Depression para: $D \rightarrow Dd$
Facilitation decay: $\tau_F\frac{dF}{dt} = 1-F$
Depression decay: $\tau_D\frac{dD}{dt} = 1-D$

Long-term

psychology <–> physiology
association <–> synapse

Origin

Aristotle
William James
Donald Hebb

Hippocampus and H.M.

Surgery to prevent continued epileptic seizures
Both hippocampi removed
Unable to learn new “declarative” information
Could learn new motor skills: golf, mirror writing

The discovery of long-term potentiation

synapses can experience long-lasting changes

Associative and Hebbian LTP

Association

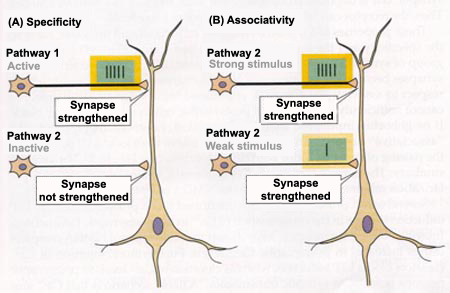
assoLTP_exp_setting assoLTP_result

Apply HF input on both weak and strong pathways can cause long-term potentiation => they are associated

Hebbian

Apply input and depolarize the neuron at the same time can have similar effect.

Spike-timing-dependent plasticity (STDP)

LTP can be temporally very precise: timing sensitive
causes earlier firing: rehearsal of a thing can be “adapted”
competition: fire early -> stronger -> fire earlier; fire late -> weaker -> fire later

Induction and expression

NMDA receptor

Long-term depression

Low frequency input will cause long-term depression in EPSP. This may support “forgetting” mechanism in memory

Intrinsic Properties

Regular spiking cell
Intrinsically bursting cell
Fast spiking cell

Cortical neuron firing patterns

firing_patterns

Diverse ion currents

$Na^+$ currents

$I_{Na,t}$: transient, rapidly activating & inactivating => action potentials
$I_{Na,p}$: persistent, noninactivating => enhances depolarization; steady-state firing

$Ca^{2+}$ currents

$I_T$(low thresh): transient; -65 mV thresh => rhythmic burst firing
$I_L$(high thresh): long-lasting, -20 mV thresh => $Ca^{2+}$ spikes that are prominent in dendrites; synaptic transmission
$I_N$: neither; rapidly inactivating, thresh -20 mV => same as $I_L$

$K^+$ currents

$I_K$: activated by strong depolarizataion => repolarization of action potential
$I_C$: activated by $[Ca^{2+}] \uparrow$ => action potential repolarization & interspike interval
$I_h$: depolarizing current, activated by hyperpolarization => rhythmic burst firing

A simple model

izhikevich

Thalamic neurons and rhythms

Two different patterns: oscillatory(bursting) tonic(transfer) modes

Intrinsic Plasticity

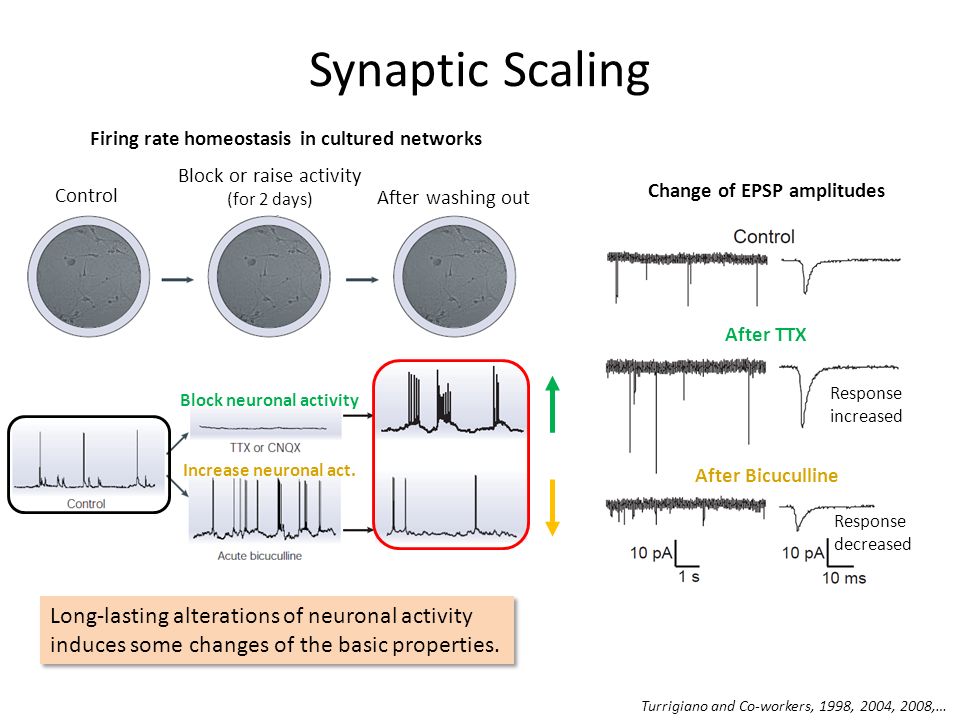
plasticityExp

It seems perhaps all currents can be up- or down-regulated depending on experience.

Network Memory: Memory and Encoding

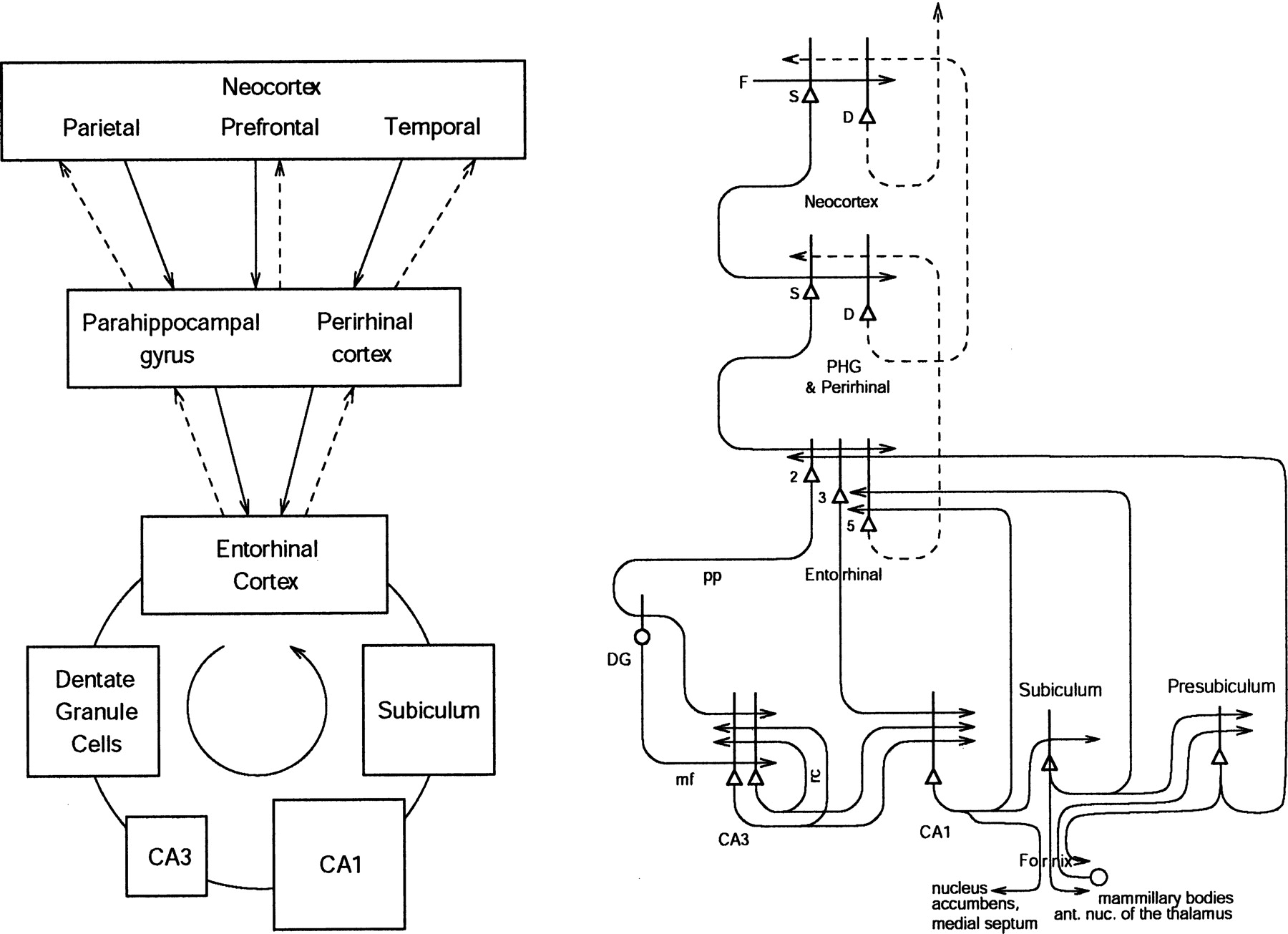
hippo_network

Autoassociative sub-network (CA3) => pattern completion
Heteroassociative sub-network (CA1, DG) => link different complex patterns
Too many memories => degradation

Hebbian Rule (Hebbian theory)

Let us assume that the persistence or repetition of a reverberatory activity (or “trace”) tends to induce lasting cellular changes that add to its stability. … When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A’s efficiency, as one of the cells firing B, is increased.

It’s just like training and testing a neural network.

Lattice Rules

Borrow the theory from ferromagnetism and lowest energy theory to explain the phenomenon in memory network.

Annealing: Ordered -heat-> Disordered -cool-> Ordered
Alternating Spins: the relationship with an atom from neighbor to distant ones are alternatively opposite and same spins.
Calculate energy: harmonious (-1), frustrated (+1)

Basic Rules

Two atoms can have:

no relationship
same spins
opposite spins

Energy Surface

we can calculate the energy of this system, by sum up the energy of each pair of atoms
system moves toward lower energy
low energy states are “attractors”

Experiment: False memory

Ramirez et al., 2013)

Emergent Properties